Okay, so today I’m gonna walk you through something I was messing with – altitude definition in science. It’s not rocket science (pun intended!), but there were a couple of gotchas I ran into, and I figured I’d share my notes.
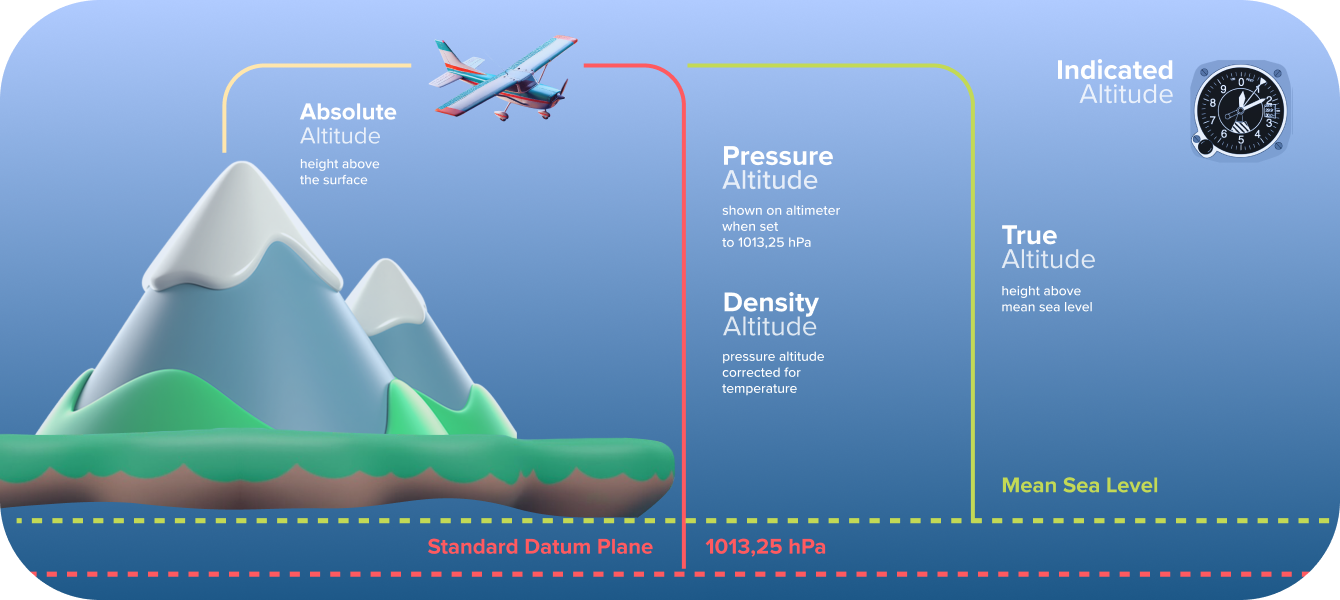
First off, I had this project where I needed to calculate some atmospheric data at different heights. Simple, right? I thought so too. Started by Googling “altitude definition science” to get a refresher. Found a bunch of stuff about mean sea level, geoid, ellipsoid… my head started spinning.
The basic problem: What “zero” altitude is? Is it sea level? But the sea isn’t flat! Is it some mathematical model of the Earth? Okay, things got complicated real fast.
Here’s what I did to get my bearings:
- Started with Mean Sea Level (MSL): I knew this was a common reference point. Basically, it’s the average sea level over a long period, taking tides and stuff into account. I grabbed some MSL data for my area from a local NOAA website – took a bit of digging, but it was there.
- Realized the Earth isn’t a perfect sphere: Obvious, I know, but the implications are important. My initial calculations were using a simplified model, and it was throwing things off.
- Looked into the Geoid: This is where it got interesting. The geoid is basically a model of the Earth’s gravity field. It represents what “sea level” would be if the oceans were extended through the continents (ignoring wind and tides, of course). Crucially, altitude above the geoid is what we often call “orthometric height”.
- Then, the Ellipsoid: This is a smooth, mathematically defined surface that approximates the Earth’s shape. GPS data often uses altitude above the ellipsoid (called “ellipsoidal height”).
Here’s the kicker: MSL, geoid, and ellipsoid are different. So, an altitude of 100 meters above MSL is not the same as 100 meters above the geoid, or 100 meters above the ellipsoid. This is what messed me up initially.
So, what did I actually do?
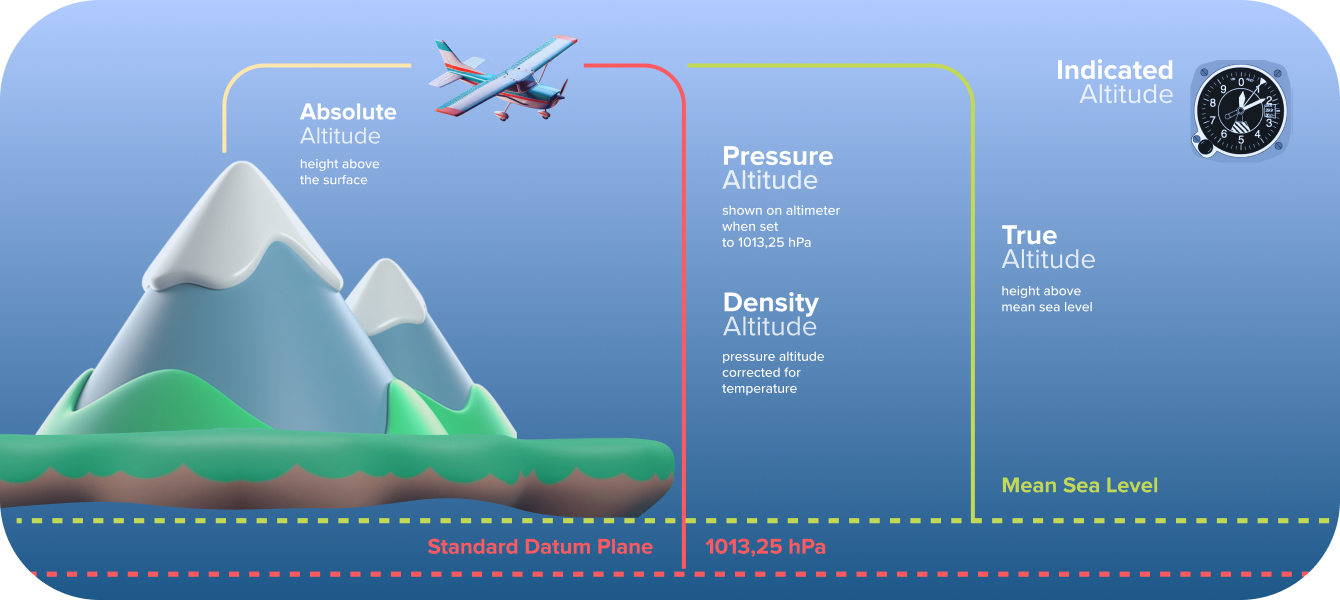
- I decided to use orthometric height (altitude above the geoid) for my calculations, because it was the most relevant for my specific atmospheric data.
- I downloaded a geoid model for my region. There are free ones available online – just gotta search.
- I had my GPS data (which gave me ellipsoidal height) – I needed to convert that to orthometric height.
- Used some Python libraries to do the conversion: I found a few that did the geoid calculations. It was a bit of trial and error to get the right one working.
- I wrote a script that took the GPS data, loaded the geoid model, and calculated the orthometric height for each point.
The Result: My data became much more consistent and accurate. Before, I had weird spikes and inconsistencies that I couldn’t explain. Now, everything lined up nicely.
The takeaway? Altitude is trickier than it looks. When dealing with any scientific data that relies on altitude, it’s important to know exactly what reference point is being used. Don’t just assume “altitude” means the same thing everywhere. Gotta dig into the details. This little adventure saved me a bunch of headaches down the road. Hope it helps you too!
